Tuning thermistor
-
Hey all, i'm reviving an old printer with a Duet2 board. A few years ago I tried to upgrade the board and struggled to find calibration files that would work. Eventually I got back around to it, and everything seems to be generally working properly now except for hotend temperature.
Its an old jhead with the original 100k thermistor (5 years old now, wow!). Digging around in the old Marlin firmware I had on the old ramps board, it looks like its a standard EPCOS 100K Thermistor, and i've set the values in the config file accordingly:
M305 P0 T100000 4092 R4700
i'm getting an interesting linear temperature deviation (measured with a thermocouple in some thermal paste around the nozel) and wondering how to correct for this:
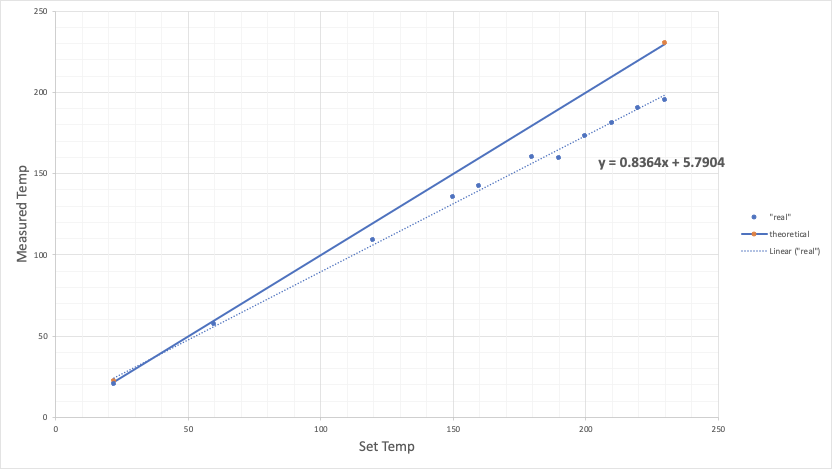
I'm wondering what this error might be indicative of. I think the setting for beta is correct, but dont really know where to start changing H and L. If anyone has anything to offer here, looking forward to hear about it!
-
the beta value only refers to the the temperature range 25-50 degrees.
as you can see from your graph, for that range its fairly accurate.
what you could do is measure the resistance at like 160 degrees and 220 degrees.
then go to https://configtool.reprapfirmware.org/Heaters click on the beta value and select custom and enter those values. it will calculate b and C which will give you a more accurate range over a large temperature range.
-
the epcos 100k is also used on the ender.
see
https://duet3d.dozuki.com/Guide/Ender+3+Pro+and+Duet+Maestro+Guide+Part+2:+Configuration/38
here the suggested values are R25 – 98801, B – 4185 -
I have found that this calculator can be illuminating: https://www.thinksrs.com/downloads/programs/therm calc/ntccalibrator/ntccalculator.html
-
@Veti I actually used the 25/100 value for B, which, sure, is far below printing temp, but is also pretty standard practice I think? At least from the web hunting i did this morning. I dont really have any way to accurately get the thermistor to high temperatures and measure its resistance.
also, I wouldnt call that large a deviation "accurate." Its 10% off at 100 degrees, if we interpolate.
-
thermistors are not that accurate.
even the same type can vary by 10% from each other.
if you want to get accurate readings, you could get for example a pt1000
i use them for my hotend and bed.I dont really have any way to accurately get the thermistor to high temperatures and measure its resistance.
you just need a multimeter. you can measure the resistance of the thermistor while its in the duet and heating. just need some point in the cable where you can attach the multimeter.
-
First I reckon everyone that has Duet board and is building a printer should have a decent multi meter with a K type thermocouple ( bead type preferred)
If you have a decent meter and thermo couple you can try this method
Loosen the screw that keeps the thermistor captured in the heater block . Slip the bead of the thermocouple under the washer and tighten slightly . You want good contact .
Pick your temp range of interest, for me it was 180 to 235 C
In Duet control Set 180 ,220 and 235 and with the meter measure actual temps for each value
You know the Steinhart model values as used in the Config file .
For each of the set temps calculate the resistance the Duet is trying to reach for each temp set in the controller using that model
see attached excel file
with calculated resistance and the correct measured temperatures goto the ThinkSRS page and recalculate R and B
It worked for me . for 180 to 235 temp deviation is only about 1 degree , originally at top end it was 10 . Room temp is a different story that's out by 10 , I get 35 instead of 25 and for me that doesn't matter
would be interested to know if this method works for others.
-
@DigiD this is a good tip I think. I've already got all the data, since I measured the temp across a variety of set points with a k type thermocouple dipped in thermal paste (thats where I got the data for the graph).
-
@DigiD Yep, this worked great! I just iterated over it a couple times and now temps are right where they should be when printing. Thanks!
-
could you post the values you found for others?
-
Hi here,
have a similar problem and didn´t want to open a new post. For the chamber and or heat-plate (Isn´t finished yet) I have bought a ntc10k from a good-know company in south-germany that makes them for ca. 30years (they do not make the ntc themself but they embed whatever ntc you like in whatever sleeve and cable you can pay for ) and I have a datasheet here. It says:
) and I have a datasheet here. It says:center-temp/R-val 25°C/10K
(r-tolerance 1%)
ß-range 25/85
ß-val 3970K
(ß-tolerance 1%)
And it comes with a table in 1°C steps with resistance for each point...What confuses me, if I enter the values for 25,85,125°C and the corresponding resistanc-values of 10000/1074,6/342,83 into here under custom https://configtool.reprapfirmware.org/Heaters it tells me
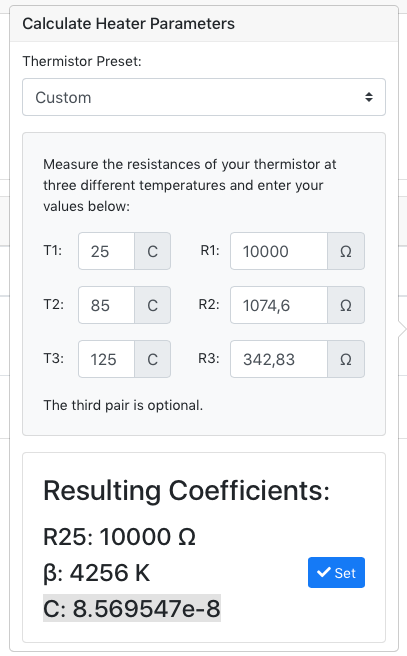
With the ß-value beeing clearly totally diffrent from the 3970 from the datasheet, while the suggested calculator here https://www.thinksrs.com/downloads/programs/therm calc/ntccalibrator/ntccalculator.html puts out the (almost) same ß-value like in the datasheet of 3970K:
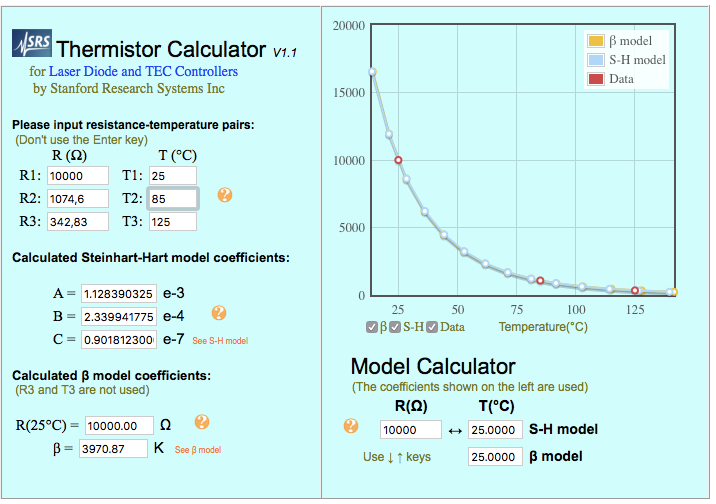
Am i missing something and this is all like it should or should the numbers in both calculators be equal?
Edit: I am new to all this Steinhart-Hart stuff and ß-val stuff so please have some patience with me

-
@LB What you are missing is that there are two distinct operating modes that both use a 'B' parameter.
If you are using simple Beta value calculation, the B parameter will represent the β value, in your case, 3970.
If you are using the steinhart-hart model (recommended because it is a better fit), the B parameter represents the reciprocal of the Steinhart-Hart B coefficient. In your example, 1/2.33994e-4 which is ~4273. The way you can tell this model is being used, is if you have a non-zero C parameter.
Unfortunately the way the information is displayed on the config tool does not make this distinction clear.
-
@Zhang-Jianyu said in Tuning thermistor:
@LB What you are missing is that there are two distinct operating modes that both use a 'B' parameter.
If you are using simple Beta value calculation, the B parameter will represent the β value, in your case, 3970.
If you are using the steinhart-hart model (recommended because it is a better fit), the B parameter represents the reciprocal of the Steinhart-Hart B coefficient. In your example, 1/2.33994e-4 which is ~4273. The way you can tell this model is being used, is if you have a non-zero C parameter.
Unfortunately the way the information is displayed on the config tool does not make this distinction clear.
Thanks so much -> That should be differentiated in the reference here https://duet3d.dozuki.com/Wiki/Gcode#Section_M308_Set_or_report_sensor_parameters
Maybe based on your wonderful description wording could be changed to something like:
- Bnnn ß-value (if used without Cnnn). If used with Cnnn the reciprocal (1/B) of the calculated Steinhart-Hart thermistor model B coefficient
And in the config-generator-webpage it should switch from "ß" to "1/B" maybe or something like it?
-
It takes some time to get a handle how everything fits together.
IIRC, a Steinhart-Hart C coefficient of 0 will result in a B coefficient that is the exact reciprocal of the β value. So the choice of using the same parameter names is probably just to simplify the implementation internally.
-
@Zhang-Jianyu said in Tuning thermistor:
It takes some time to get a handle how everything fits together.
IIRC, a Steinhart-Hart C coefficient of 0 will result in a B coefficient that is the exact reciprocal of the β value. So the choice of using the same parameter names is probably just to simplify the implementation internally.
Thanks so much - I cannot follow your explanation here "a Steinhart-Hart C coefficient of 0 will result in a B coefficient that is the exact reciprocal of the β value" but maybe you can elaborate?
Much more important for me right now:
The C-values on both calculators differ also! What do you think regarding this, is it maybe that the webcalculator just uses less digits or something similar or can you "spot" any mistake in my input that could be the reason for it?
(also I still do not get the reciprocal-formula, because 1/(2.339941775e-4) on my computer-calculator spill out 0,000004273610612?)
-
For the reciprocal I am using dot '.' as a decimal separator. Since you use comma decimal separator ',' you'll need to put that in instead.
So the corrected one for you will be
1/2,3399e-4Regarding the slight difference in output, it's likely just due to the precision of the calculations on the computer.
The bit about the 1/B and β being equal is not of real practical use but I find it interesting

-
@LB said in Tuning thermistor:
The C-values on both calculators differ also! What do you think regarding this, is it maybe that the webcalculator just uses less digits or something similar or can you "spot" any mistake in my input that could be the reason for it?
Can you elaborate? How much do they differ by?
-
@Zhang-Jianyu said in Tuning thermistor:
For the reciprocal I am using dot '.' as a decimal separator. Since you use comma decimal separator ',' you'll need to put that in instead.
Ah thanks, I fall into the old "." & "," trap *- slap on the head- * O.K. now

@dc42 said in Tuning thermistor:
@LB said in Tuning thermistor:
The C-values on both calculators differ also! What do you think regarding this, is it maybe that the webcalculator just uses less digits or something similar or can you "spot" any mistake in my input that could be the reason for it?
Can you elaborate? How much do they differ by?
now the reciprocal B-Value from "SRS"-calculator (see pictures posted before in this thread) 1/(2,339941775e-4) evaluates on my comp-calc to 4273,6 which is reasonably close to the 4256 from the reprap-configtool, but is not the same. Or did I do again something wrong?
Also the C is for
SRS-Calculator (see pictures posted before in this thread)
0.9018123000e-7, with swapped ,/. is 0,000 000 090 181 23
but in the reprap-configtool (see pictures posted before in this thread)
8.569547e-8, with swapped ,/. is 0,000 000 085 695 47
though they are close they differ a bit.@Zhang-Jianyu said in Tuning thermistor:
Regarding the slight difference in output, it's likely just due to the precision of the calculations on the computer.
Did I do something wrong or is it maybe realted to the size like double-float or something in the web-calculation? Since values are close but do not match something like resolution/precision might be the case? I guess now thanks to you I know how to use the calculator I would go with the SRS?
Thanks anyway, for getting me started! Since I know now how to use the SRS-Calculator I can put its values in the config.g

-
SRS calc is this:
C =((1/T1-1/T2)-(Math.log(R1)- Math.log(R2))*(1/T1-1/T3)/(Math.log(R1)-Math.log(R3)))/((Math.pow(Math.log(R1),3)-Math.pow(Math.log(R2),3)) - (Math.log(R1)-Math.log(R2))*(Math.pow(Math.log(R1),3)-Math.pow(Math.log(R3),3))/(Math.log(R1)-Math.log(R3))); B =((1/T1-1/T2)-C*(Math.pow(Math.log(R1),3)-Math.pow(Math.log(R2),3)))/(Math.log(R1)-Math.log(R2)); A = 1/T1-C*(Math.log(R1))*(Math.log(R1))*(Math.log(R1))-B*Math.log(R1); -
@Zhang-Jianyu said in Tuning thermistor:
SRS calc is this:
C =((1/T1-1/T2)-(Math.log(R1)- Math.log(R2))*(1/T1-1/T3)/(Math.log(R1)-Math.log(R3)))/((Math.pow(Math.log(R1),3)-Math.pow(Math.log(R2),3)) - (Math.log(R1)-Math.log(R2))*(Math.pow(Math.log(R1),3)-Math.pow(Math.log(R3),3))/(Math.log(R1)-Math.log(R3))); B =((1/T1-1/T2)-C*(Math.pow(Math.log(R1),3)-Math.pow(Math.log(R2),3)))/(Math.log(R1)-Math.log(R2)); A = 1/T1-C*(Math.log(R1))*(Math.log(R1))*(Math.log(R1))-B*Math.log(R1);Wow - thanks

Looks a bit different then the easy "mouse-over"-formula SRS blends in... Maybe I just copy and past it into "processing" (the only thing I know) and see how much influence the variable-room has, or maybe even de-/shift with multiplier/divider?