As of RRF v3.1.1, we can pass G31 a temperature coefficient, C, when using an inductive probe like a PINDA v2 to offset the probe's variance at different temperatures. In practice, though, the relationship isn't linear, and the temperature effect yields increasing offsets at higher temperatures.
How about an additional optional parameter, (D?), that is the factor for a second-degree polynomial for temperature compensation? The additional compensated height would then be C * temp + D * temp^2.
I find that I can sufficiently approximate the relationship with a second-degree polynomial. (A third-degree polynomial is better, but second-degree gets close enough for FFF printing.)
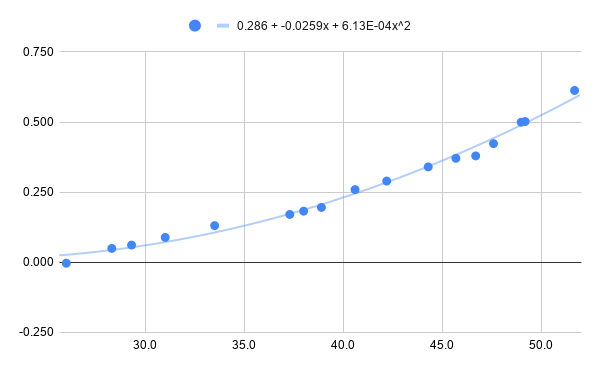
I model this (messily!) in RRF3 with some conditional GCode. I have a G831.g script that approximates the model with a series of short linear segments, and call it just before homing Z, leveling the bed, or measuring a mesh:
if sensors.analog[2].lastReading < 25 ; temp < 25°C
G31 P500 X23 Y5 Z{ 0.65 + 0.000 } H2 S20 C0.001685
elif sensors.analog[2].lastReading < 30 ; 25 <= temp < 30
G31 P500 X23 Y5 Z{ 0.65 + 0.008425 } H2 S25 C0.007815
elif sensors.analog[2].lastReading < 35 ; 30 <= temp < 35
G31 P500 X23 Y5 Z{ 0.65 + 0.047500 } H2 S30 C0.013945
elif sensors.analog[2].lastReading < 40 ; 35 <= temp < 40
G31 P500 X23 Y5 Z{ 0.65 + 0.117225 } H2 S35 C0.020075
elif sensors.analog[2].lastReading < 45 ; 40 <= temp < 45
G31 P500 X23 Y5 Z{ 0.65 + 0.217600 } H2 S40 C0.026205
elif sensors.analog[2].lastReading < 50 ; 45 <= temp < 50
G31 P500 X23 Y5 Z{ 0.65 + 0.348625 } H2 S45 C0.032335
elif sensors.analog[2].lastReading < 55 ; 50 <= temp < 55
G31 P500 X23 Y5 Z{ 0.65 + 0.510300 } H2 S50 C0.038465
elif sensors.analog[2].lastReading < 60 ; 55 <= temp < 60
G31 P500 X23 Y5 Z{ 0.65 + 0.702625 } H2 S55 C0.044595
elif sensors.analog[2].lastReading < 65 ; 60 <= temp < 65
G31 P500 X23 Y5 Z{ 0.65 + 0.925600 } H2 S60 C0.050725
else ; 65 <= temp
G31 P500 X23 Y5 Z{ 0.65 + 1.179225 } H2 S65 C0.056855
This works pretty well, but it is a bit hacky. I find myself sprinkling G831 calls all over homez.g, homeall.g, bed.g, print start scripts, etc. A polynomial factor would be easier and cleaner.
(One more parameter -- E? -- would be even better, for C * temp + D * temp^2 + E * temp^3, but hey, I don't want to get greedy here. At least on my machine, the 2nd-degree approximation gets within 0.01mm error for the usable temperature range.)


 )
)
